
문제 1
1.1: 1개, 2개, 4개, 8개의 코어를 사용하는 경우, 프로그램의 실행시간은 얼마인가?
[풀이]
CPI란, 명령어 하나를 처리하는데 필요한 클럭 사이클 수를 의미한다.
문제에서 주어진 프로세서에 대해 정리하자면 다음과 같다.
| 산술 명령어 | 적재/저장 명령어 | 분기 명령어 | |
| CPI | 1 | 12 | 5 |
| 명령어 개수 | 2.56E9(2.56x109) | 1.28E9 | 2.56E8 |
프로세서는 2GHz 의 클럭 주파수로 동작하는데, 이는 1초에 클럭 사이클이 2*10^9번 임을 뜻하며 클럭 속도가 2*10^9 라는 말과 같다(1GHz = 10^9).
프로그램의 실행시간 = CPU 클럭 사이클 수 / 클럭 속도
= CPU 클럭 사이클 수 * 클럭 사이클 시간
CPU 클럭 사이클 수 = 명령어의 수(IC) * CPI
프로그램의 실행시간을 구하는 과정은 아래와 같다.


따라서 1개의 코어를 사용하는 경우 프로그램의 실행시간은 9.6
2개의 코어를 사용하는 경우 프로그램의 실행시간은 7.04
4개의 코어를 사용하는 경우 프로그램의 실행시간은 3.84
8개의 코어를 사용하는 경우 프로그램의 실행시간은 2.24
이며 코어를 여러 개 사용할수록 프로그램의 실행시간이 줄어든다는 것을 알 수 있고 성능비교는 다음과 같다.
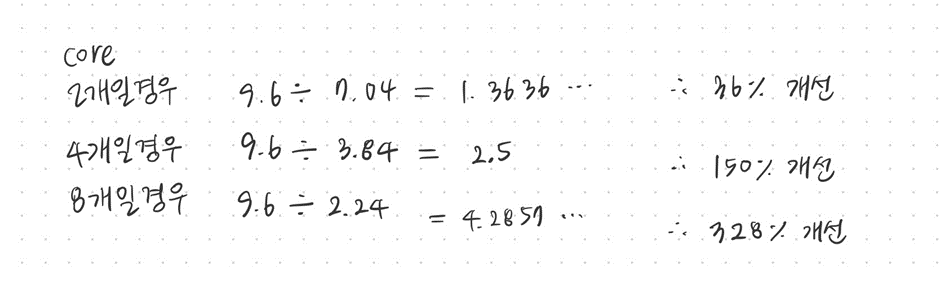
1.2: 산술 연산의 CPI가 2배가 되었다면 1개, 2개, 4개, 8개의 프로세서에서 프로그램의 실행시간은 어떻게 변화하는가?
[풀이]
산술연산의 CPI를 2배로 수정해주면 아래표와 같다.
| 산술 명령어 | 적재/저장 명령어 | 분기 명령어 | |
| CPI | 2 | 12 | 5 |
| 명령어 개수 | 2.56E9(2.56x109) | 1.28E9 | 2.56E8 |
그리고 프로그램 실행시간을 구하는 과정은 아래와 같다.

따라서 1개의 코어를 사용하는 경우 프로그램의 실행시간은 10.88
2개의 코어를 사용하는 경우 프로그램의 실행시간은 7.954285714
4개의 코어를 사용하는 경우 프로그램의 실행시간은 4.297142857
8개의 코어를 사용하는 경우 프로그램의 실행시간은 2.468571429
산술연산의 CPI가 기존의 CPI였을 때와 2배가 되었을 때의 실행시간을 비교하면 아래 표와 같다.
| 산술연산의 CPI가 1 일 때 (원래의 CPI) |
산술연산의 CPI가 2 일 때 (2배한 CPI) |
|
| 코어 1개 | 9.6 | 10.88 |
| 코어 2개 | 7.04 | 7.954285714 |
| 코어 4개 | 3.84 | 4.297142857 |
| 코어 8개 | 2.24 | 2.468571429 |
성능을 비교해보면
코어 1개일 때 13% 감소
코어 2개일 때 12% 감소
코어 3개일 때 11% 감소
코어 4개일 때 10% 감소 이다.
1.3: 원래 CPI를 가지고 4개의 프로세서에서 얻은 성능과 같은 성능을 단일 프로세서에서 얻으려고 한다면 적재/저장 명령어의 CPI는 얼마가 되어야 하는가?
[풀이]
원래의 CPI를 가지고 4개의 프로세서에서 얻은 실행시간은 3.84이다.
구하는 과정은 아래와 같다.

따라서 1개의 프로세서에서 같은 실행시간이 나오게 하려면 적재/저장 명령어의 CPI는 3이 되어야 한다.

문제 2
2.1: 프로그램을 2배 빠르게 하고 싶으면 FP 명령어의 CPI를 얼마나 개선하여야 하는가?
[풀이]
문제에서 주어진 프로세서에 대해 정리하자면 다음과 같다.
| FP 명령어 | INT 명령어 | 적재/저장 명령어 | 분기 명령어 | |
| CPI | 1 | 1 | 4 | 2 |
| 명령어 개수 | 56*10^6 | 110*10^6 | 80*10^6 | 16*10^6 |
마지막 식을 보면 우변의 값이 음수이므로 x가 음수여야 하는데, FP명령어의 CPI는 음수가 될 수 없으므로, 문제에서 주어진 조건을 만족하는 FP명령어 CPI는 없다(구하지 못한다).
2.2: 프로그램을 2배 빠르게 하고 싶으면 적재/저장 명령어의 CPI를 얼마나 개선하여야 하는가?
[풀이]
CPI를 얼마나 개선해야 하는지를 알아보기 위해서 기존의 적재/저장 명령어 CPI인 4를 x값인 0.7625로 나누어 보면 5.2459… 값이 나온다. 따라서 CPI를 약 5배개선 시켜야 한다.
2.3: INT, FP 명령어의 CPI가 40% 줄고, 적재/저장 명령어와 분기 명령어의 CPI가 30% 줄면 프로그램의 실행시간은 얼마나 개선되는가?
[풀이]
INT 명령어와 FP 명령어의 CPI가 40%가 줄었다고 했으므로 0.6를 곱하고, 적재/저장 명령어와 분기 명령어의 CPI가 30% 줄었다고 했으므로 0.7을 곱하면 다음 표와 같다.
| FP 명령어 | INT 명령어 | 적재/저장 명령어 | 분기 명령어 | |
| CPI | 0.6 | 0.6 | 2.8 | 1.4 |
| 명령어 개수 | 56*10^6 | 110*10^6 | 80*10^6 | 16*10^6 |
수정된 CPI 값이 반영된 실행시간을 구하면 다음과 같다.
따라서 약 1.5배 개선되었다.
문제 2
2.1: 프로그램을 2배 빠르게 하고 싶으면 FP 명령어의 CPI를 얼마나 개선하여야 하는가?
[풀이]
문제에서 주어진 프로세서에 대해 정리하자면 다음과 같다.
| FP 명령어 | INT 명령어 | 적재/저장 명령어 | 분기 명령어 | |
| CPI | 1 | 1 | 4 | 2 |
| 명령어 개수 | 56*10^6 | 110*10^6 | 80*10^6 | 16*10^6 |
마지막 식을 보면 우변의 값이 음수이므로 x가 음수여야 하는데, FP명령어의 CPI는 음수가 될 수 없으므로, 문제에서 주어진 조건을 만족하는 FP명령어 CPI는 없다(구하지 못한다).
2.2: 프로그램을 2배 빠르게 하고 싶으면 적재/저장 명령어의 CPI를 얼마나 개선하여야 하는가?
[풀이]
CPI를 얼마나 개선해야 하는지를 알아보기 위해서 기존의 적재/저장 명령어 CPI인 4를 x값인 0.7625로 나누어 보면 5.2459… 값이 나온다. 따라서 CPI를 약 5배개선 시켜야 한다.
2.3: INT, FP 명령어의 CPI가 40% 줄고, 적재/저장 명령어와 분기 명령어의 CPI가 30% 줄면 프로그램의 실행시간은 얼마나 개선되는가?
[풀이]
INT 명령어와 FP 명령어의 CPI가 40%가 줄었다고 했으므로 0.6를 곱하고, 적재/저장 명령어와 분기 명령어의 CPI가 30% 줄었다고 했으므로 0.7을 곱하면 다음 표와 같다.
| FP 명령어 | INT 명령어 | 적재/저장 명령어 | 분기 명령어 | |
| CPI | 0.6 | 0.6 | 2.8 | 1.4 |
| 명령어 개수 | 56*10^6 | 110*10^6 | 80*10^6 | 16*10^6 |
수정된 CPI 값이 반영된 실행시간을 구하면 다음과 같다.
따라서 약 1.5배 개선되었다.
문제 2
2.1: 프로그램을 2배 빠르게 하고 싶으면 FP 명령어의 CPI를 얼마나 개선하여야 하는가?
[풀이]
문제에서 주어진 프로세서에 대해 정리하자면 다음과 같다.
| FP 명령어 | INT 명령어 | 적재/저장 명령어 | 분기 명령어 | |
| CPI | 1 | 1 | 4 | 2 |
| 명령어 개수 | 56*10^6 | 110*10^6 | 80*10^6 | 16*10^6 |
마지막 식을 보면 우변의 값이 음수이므로 x가 음수여야 하는데, FP명령어의 CPI는 음수가 될 수 없으므로, 문제에서 주어진 조건을 만족하는 FP명령어 CPI는 없다(구하지 못한다).
2.2: 프로그램을 2배 빠르게 하고 싶으면 적재/저장 명령어의 CPI를 얼마나 개선하여야 하는가?
[풀이]
CPI를 얼마나 개선해야 하는지를 알아보기 위해서 기존의 적재/저장 명령어 CPI인 4를 x값인 0.7625로 나누어 보면 5.2459… 값이 나온다. 따라서 CPI를 약 5배개선 시켜야 한다.
2.3: INT, FP 명령어의 CPI가 40% 줄고, 적재/저장 명령어와 분기 명령어의 CPI가 30% 줄면 프로그램의 실행시간은 얼마나 개선되는가?
[풀이]
INT 명령어와 FP 명령어의 CPI가 40%가 줄었다고 했으므로 0.6를 곱하고, 적재/저장 명령어와 분기 명령어의 CPI가 30% 줄었다고 했으므로 0.7을 곱하면 다음 표와 같다.
| FP 명령어 | INT 명령어 | 적재/저장 명령어 | 분기 명령어 | |
| CPI | 0.6 | 0.6 | 2.8 | 1.4 |
| 명령어 개수 | 56*10^6 | 110*10^6 | 80*10^6 | 16*10^6 |
수정된 CPI 값이 반영된 실행시간을 구하면 다음과 같다.
따라서 약 1.5배 개선되었다.

문제 1
1.1: 1개, 2개, 4개, 8개의 코어를 사용하는 경우, 프로그램의 실행시간은 얼마인가?
[풀이]
CPI란, 명령어 하나를 처리하는데 필요한 클럭 사이클 수를 의미한다.
문제에서 주어진 프로세서에 대해 정리하자면 다음과 같다.
| 산술 명령어 | 적재/저장 명령어 | 분기 명령어 | |
| CPI | 1 | 12 | 5 |
| 명령어 개수 | 2.56E9(2.56x109) | 1.28E9 | 2.56E8 |
프로세서는 2GHz 의 클럭 주파수로 동작하는데, 이는 1초에 클럭 사이클이 2*10^9번 임을 뜻하며 클럭 속도가 2*10^9 라는 말과 같다(1GHz = 10^9).
프로그램의 실행시간 = CPU 클럭 사이클 수 / 클럭 속도
= CPU 클럭 사이클 수 * 클럭 사이클 시간
CPU 클럭 사이클 수 = 명령어의 수(IC) * CPI
프로그램의 실행시간을 구하는 과정은 아래와 같다.


따라서 1개의 코어를 사용하는 경우 프로그램의 실행시간은 9.6
2개의 코어를 사용하는 경우 프로그램의 실행시간은 7.04
4개의 코어를 사용하는 경우 프로그램의 실행시간은 3.84
8개의 코어를 사용하는 경우 프로그램의 실행시간은 2.24
이며 코어를 여러 개 사용할수록 프로그램의 실행시간이 줄어든다는 것을 알 수 있고 성능비교는 다음과 같다.
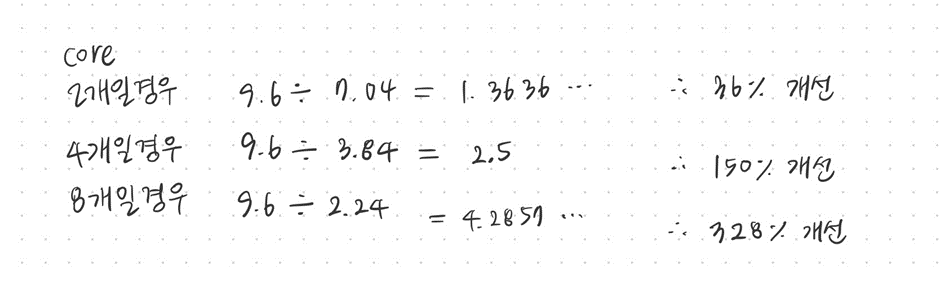
1.2: 산술 연산의 CPI가 2배가 되었다면 1개, 2개, 4개, 8개의 프로세서에서 프로그램의 실행시간은 어떻게 변화하는가?
[풀이]
산술연산의 CPI를 2배로 수정해주면 아래표와 같다.
| 산술 명령어 | 적재/저장 명령어 | 분기 명령어 | |
| CPI | 2 | 12 | 5 |
| 명령어 개수 | 2.56E9(2.56x109) | 1.28E9 | 2.56E8 |
그리고 프로그램 실행시간을 구하는 과정은 아래와 같다.

따라서 1개의 코어를 사용하는 경우 프로그램의 실행시간은 10.88
2개의 코어를 사용하는 경우 프로그램의 실행시간은 7.954285714
4개의 코어를 사용하는 경우 프로그램의 실행시간은 4.297142857
8개의 코어를 사용하는 경우 프로그램의 실행시간은 2.468571429
산술연산의 CPI가 기존의 CPI였을 때와 2배가 되었을 때의 실행시간을 비교하면 아래 표와 같다.
| 산술연산의 CPI가 1 일 때 (원래의 CPI) |
산술연산의 CPI가 2 일 때 (2배한 CPI) |
|
| 코어 1개 | 9.6 | 10.88 |
| 코어 2개 | 7.04 | 7.954285714 |
| 코어 4개 | 3.84 | 4.297142857 |
| 코어 8개 | 2.24 | 2.468571429 |
성능을 비교해보면
코어 1개일 때 13% 감소
코어 2개일 때 12% 감소
코어 3개일 때 11% 감소
코어 4개일 때 10% 감소 이다.
1.3: 원래 CPI를 가지고 4개의 프로세서에서 얻은 성능과 같은 성능을 단일 프로세서에서 얻으려고 한다면 적재/저장 명령어의 CPI는 얼마가 되어야 하는가?
[풀이]
원래의 CPI를 가지고 4개의 프로세서에서 얻은 실행시간은 3.84이다.
구하는 과정은 아래와 같다.

따라서 1개의 프로세서에서 같은 실행시간이 나오게 하려면 적재/저장 명령어의 CPI는 3이 되어야 한다.

문제 2
2.1: 프로그램을 2배 빠르게 하고 싶으면 FP 명령어의 CPI를 얼마나 개선하여야 하는가?
[풀이]
문제에서 주어진 프로세서에 대해 정리하자면 다음과 같다.
| FP 명령어 | INT 명령어 | 적재/저장 명령어 | 분기 명령어 | |
| CPI | 1 | 1 | 4 | 2 |
| 명령어 개수 | 56*10^6 | 110*10^6 | 80*10^6 | 16*10^6 |
마지막 식을 보면 우변의 값이 음수이므로 x가 음수여야 하는데, FP명령어의 CPI는 음수가 될 수 없으므로, 문제에서 주어진 조건을 만족하는 FP명령어 CPI는 없다(구하지 못한다).
2.2: 프로그램을 2배 빠르게 하고 싶으면 적재/저장 명령어의 CPI를 얼마나 개선하여야 하는가?
[풀이]
CPI를 얼마나 개선해야 하는지를 알아보기 위해서 기존의 적재/저장 명령어 CPI인 4를 x값인 0.7625로 나누어 보면 5.2459… 값이 나온다. 따라서 CPI를 약 5배개선 시켜야 한다.
2.3: INT, FP 명령어의 CPI가 40% 줄고, 적재/저장 명령어와 분기 명령어의 CPI가 30% 줄면 프로그램의 실행시간은 얼마나 개선되는가?
[풀이]
INT 명령어와 FP 명령어의 CPI가 40%가 줄었다고 했으므로 0.6를 곱하고, 적재/저장 명령어와 분기 명령어의 CPI가 30% 줄었다고 했으므로 0.7을 곱하면 다음 표와 같다.
| FP 명령어 | INT 명령어 | 적재/저장 명령어 | 분기 명령어 | |
| CPI | 0.6 | 0.6 | 2.8 | 1.4 |
| 명령어 개수 | 56*10^6 | 110*10^6 | 80*10^6 | 16*10^6 |
수정된 CPI 값이 반영된 실행시간을 구하면 다음과 같다.
따라서 약 1.5배 개선되었다.
문제 2
2.1: 프로그램을 2배 빠르게 하고 싶으면 FP 명령어의 CPI를 얼마나 개선하여야 하는가?
[풀이]
문제에서 주어진 프로세서에 대해 정리하자면 다음과 같다.
| FP 명령어 | INT 명령어 | 적재/저장 명령어 | 분기 명령어 | |
| CPI | 1 | 1 | 4 | 2 |
| 명령어 개수 | 56*10^6 | 110*10^6 | 80*10^6 | 16*10^6 |
마지막 식을 보면 우변의 값이 음수이므로 x가 음수여야 하는데, FP명령어의 CPI는 음수가 될 수 없으므로, 문제에서 주어진 조건을 만족하는 FP명령어 CPI는 없다(구하지 못한다).
2.2: 프로그램을 2배 빠르게 하고 싶으면 적재/저장 명령어의 CPI를 얼마나 개선하여야 하는가?
[풀이]
CPI를 얼마나 개선해야 하는지를 알아보기 위해서 기존의 적재/저장 명령어 CPI인 4를 x값인 0.7625로 나누어 보면 5.2459… 값이 나온다. 따라서 CPI를 약 5배개선 시켜야 한다.
2.3: INT, FP 명령어의 CPI가 40% 줄고, 적재/저장 명령어와 분기 명령어의 CPI가 30% 줄면 프로그램의 실행시간은 얼마나 개선되는가?
[풀이]
INT 명령어와 FP 명령어의 CPI가 40%가 줄었다고 했으므로 0.6를 곱하고, 적재/저장 명령어와 분기 명령어의 CPI가 30% 줄었다고 했으므로 0.7을 곱하면 다음 표와 같다.
| FP 명령어 | INT 명령어 | 적재/저장 명령어 | 분기 명령어 | |
| CPI | 0.6 | 0.6 | 2.8 | 1.4 |
| 명령어 개수 | 56*10^6 | 110*10^6 | 80*10^6 | 16*10^6 |
수정된 CPI 값이 반영된 실행시간을 구하면 다음과 같다.
따라서 약 1.5배 개선되었다.
문제 2
2.1: 프로그램을 2배 빠르게 하고 싶으면 FP 명령어의 CPI를 얼마나 개선하여야 하는가?
[풀이]
문제에서 주어진 프로세서에 대해 정리하자면 다음과 같다.
| FP 명령어 | INT 명령어 | 적재/저장 명령어 | 분기 명령어 | |
| CPI | 1 | 1 | 4 | 2 |
| 명령어 개수 | 56*10^6 | 110*10^6 | 80*10^6 | 16*10^6 |
마지막 식을 보면 우변의 값이 음수이므로 x가 음수여야 하는데, FP명령어의 CPI는 음수가 될 수 없으므로, 문제에서 주어진 조건을 만족하는 FP명령어 CPI는 없다(구하지 못한다).
2.2: 프로그램을 2배 빠르게 하고 싶으면 적재/저장 명령어의 CPI를 얼마나 개선하여야 하는가?
[풀이]
CPI를 얼마나 개선해야 하는지를 알아보기 위해서 기존의 적재/저장 명령어 CPI인 4를 x값인 0.7625로 나누어 보면 5.2459… 값이 나온다. 따라서 CPI를 약 5배개선 시켜야 한다.
2.3: INT, FP 명령어의 CPI가 40% 줄고, 적재/저장 명령어와 분기 명령어의 CPI가 30% 줄면 프로그램의 실행시간은 얼마나 개선되는가?
[풀이]
INT 명령어와 FP 명령어의 CPI가 40%가 줄었다고 했으므로 0.6를 곱하고, 적재/저장 명령어와 분기 명령어의 CPI가 30% 줄었다고 했으므로 0.7을 곱하면 다음 표와 같다.
| FP 명령어 | INT 명령어 | 적재/저장 명령어 | 분기 명령어 | |
| CPI | 0.6 | 0.6 | 2.8 | 1.4 |
| 명령어 개수 | 56*10^6 | 110*10^6 | 80*10^6 | 16*10^6 |
수정된 CPI 값이 반영된 실행시간을 구하면 다음과 같다.
따라서 약 1.5배 개선되었다.
