참고영상
이번엔 cost function과 cost 를 최소화하는 gradient decent 에 대해 정리하려고 한다.

저번에 linear hypothesis 일때에는 저런모양으로 그래프가 나타났었다
이것의 장점은 어느곳에서 시작하던지 최소값을 갖는 w(weight)을 알아낼 수 있다는 것!
근데 이제 우리의 H(x) 꼴이 좀 변화했다!(sigmoid 함수를 이용하기로 했었다)

우리는 0과 1사이의 결과만 나오길 바랐기 때문에 오른쪽 처럼 H(x)를 적어줬었다.
그런데 이건 cost function을 그려보면 저렇게 울퉁~ 불퉁~ 하다
저러면 문제가 어느 점에서 시작하느냐에 따라서 최저점에 도착하는게 다 다를 수 있다.

이런 지점을 local minimum 이라고 하고, 우리가 최종적으로 찾고자 하는 건 global minimum 이라고 한다.
여튼 이런 모양의 그래프는 우리가 사용할 수 없다는거다.
prediction을 제대로 못할테니까
hypothesis 를 좀 바꿨던 것 처럼 cost funciton도 손을 대야 한다.
먼저 뭔지부터 보자
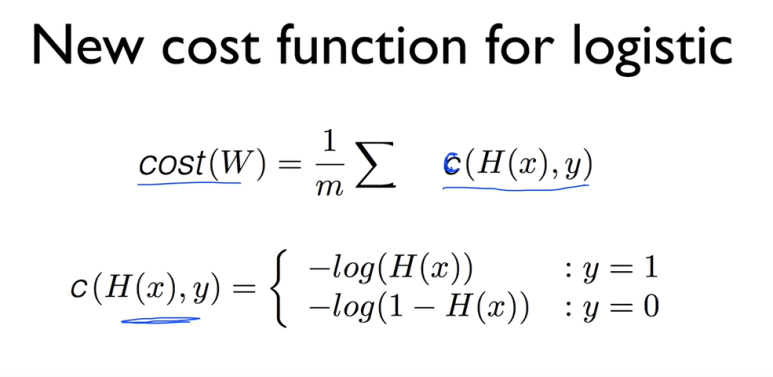
저렇게 놔야하는 이유는 뭘까?

일단 log 함수를 쓰는 이유!
저 Hypothesis가 저런 식이었는데 그래프를 울퉁불퉁하게 만드는 역할이 e^-2 이다
저것과 상극이 되는게 log 함수여서 사용한다는 아이디어..

왼쪽에 있는 그래프는 -log(x) 이다
y = 1 이라고 했을때
H(x) (= z) 의 값을 1로 했을 땐 cost가 0이고
0으로 했을 땐 cost가 무한대이다.
반대로 오른쪽의 그래프는 -log(1-x)인데
y=0이라고 할때
z의 값이 0일땐 cost가 0이고
z의 값이 1일땐 cost가 무한대 이다.
이 두 그래프를 합친다면 이전에 우리가 얻었던 그래프마냥 매끈하게 그려질 것이다.
-> 경사타고 내려가기가 적용 가능하다
총 정리를 해보자면

저렇게 네모표시한것처럼 한줄로 표현이 가능할 것이다.
어차피 y=1 일때에는 뒤에 있는 항이 사라지고
y=0일때에는 앞에 있는 항이 사라지기 때문이다.
그럼 이제 cost 를 minimize 하는 일만 남았다

전에 했던것처럼 경사타고 내려가기 하면된다.
저런 미분 같은건 직접X , 컴퓨터가 해주니까.. 하면되고 .
tensorflow로 할때

코드로 구현한다면 이렇게 하면 되겠지
어차피 GradientDescentOptimizer()라는 라이브러리가 있기때문에 갖다 쓰면 된다.
