지난번에는 XOR 문제를 두개의 유닛으로 구성된 neural network으로 풀수 있다는 것을 알아보았다
대신 w와 b는 주어졌었는데
이 값들을 어떻게 자동적(기계적으로) 학습할 수 있을까 이번 강의의 주제.

w의 값이 어디서 시작하든 cost함수에서 기울기를 구해서 계속 내려가면 global minimum에 도달할 수 있을 것이다
이것을 구현하기 위해선 미분값이 필요하다

어떤 예측한 값과 원하는 값의 차이 error을 앞으로 돌려서 다시 계산하는 알고리즘
Back propagation

저 수식을 그림으로 나타내면 이렇게 되고
chain rule은

이런걸 말한다
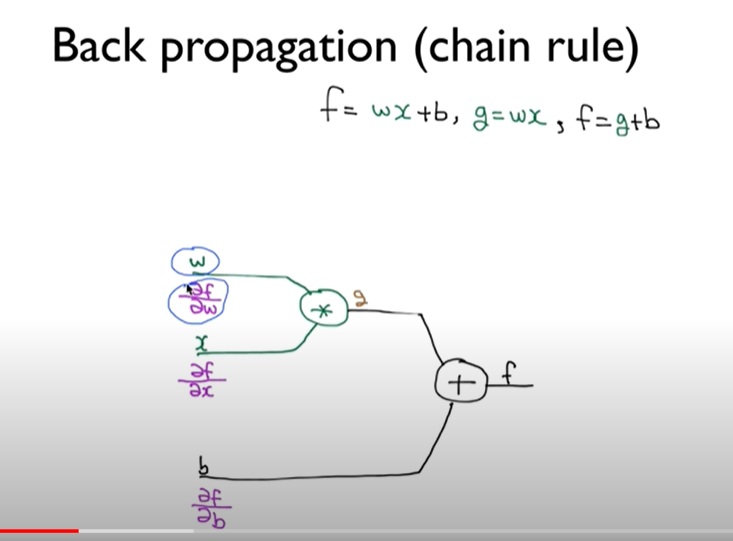
저런 w 같은 것들이 f에 미치는 영향을 알아보려면 미분값이 필요할거다
방법은 두가지 이다

w와 x,b를 받아서 그래프에 입력시키고 backward로 실제 미분의 값을 계산한다

그러기 위해선 x와 w를 저렇게 나타내준다

g가 f에 미치는 영향은 1
b가 미치는 영향도 1

이번에는 w에 관한 값을 구하고 싶다.
이럴때 chain rule을 사용한다

이렇게
af/ax도 구해보자


-2가 된다

한가지 경우를 살펴봤었는데 이번엔 좀 복잡한 경우가 있다고 생각하자
가장 마지막에 있는 노드를 계산한다
a가 f에 미치는 영향을 구할 수 있겠지
그 값을 구한다. 그리고 back propagation을 진행시킨다.
g 까지 가겠지


텐서플로우에서 back propagation 을 하는것

그리고 cost 함수의 미분값이 중요하다
텐서플로우에서는 각각을 그래프로 나누어서 한다
미분을 하기 위해서 이다
근데 구현할 필요가 없고 텐서보드라는 곳에서 그래프를 볼 수 있다.

이런 방법으로 아무리 복잡해도 간단하게 back propagation을 통해 미분값을 구할 수 있다는 것이다
