별도의 test set으로 모델을 평가해보고 learning rate에 대해서 알아보자

이제부터는 data를 training 이랑 test로 datasets를 나누는 거다
training set으로 학습을 하고
test set으로 (모델에게는 새로운 데이터) 모델을 평가하는 것이다.
y_data는 one-hot으로 주어지는 것 같다.

전체코드는 이러할 것이다.
출력되는 prediction 과 accuracy 는 test data를 기반으로 한 것이기 때문에 의미가 있다
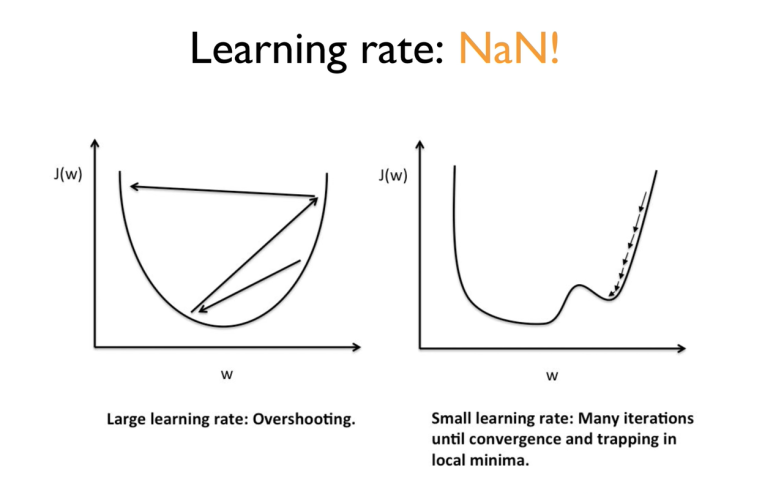
예전에는 learning rate를 0.01로 주고 넘어가고 그랬었지.
근데 이걸 어떻게 설정하느냐에 따라서 문제가 생길 수있다.
값이 너무 크다면 step이 큰거니까 왼쪽 그림과 같은 상황이 나타날 수 있다.-> 발산
반대로 learning rate을 너무 작게 주면 오른쪽 그림과 같이 나타날 수 있다.
학습이 더디다. 그리고 중간에 굴곡이 조금이라도 있으면 최저점인줄 알고 착각할 수도 있다.
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
x_data = [[1, 2, 1],
[1, 3, 2],
[1, 3, 4],
[1, 5, 5],
[1, 7, 5],
[1, 2, 5],
[1, 6, 6],
[1, 7, 7]]
y_data = [[0, 0, 1],
[0, 0, 1],
[0, 0, 1],
[0, 1, 0],
[0, 1, 0],
[0, 1, 0],
[1, 0, 0],
[1, 0, 0]]
# Evaluation our model using this test dataset
x_test = [[2, 1, 1],
[3, 1, 2],
[3, 3, 4]]
y_test = [[0, 0, 1],
[0, 0, 1],
[0, 0, 1]]
X = tf.placeholder("float", [None, 3])
Y = tf.placeholder("float", [None, 3])
W = tf.Variable(tf.random_normal([3, 3]))
b = tf.Variable(tf.random_normal([3]))
# tf.nn.softmax computes softmax activations
# softmax = exp(logits) / reduce_sum(exp(logits), dim)
hypothesis = tf.nn.softmax(tf.matmul(X, W) + b)
# Cross entropy cost/loss
cost = tf.reduce_mean(-tf.reduce_sum(Y * tf.log(hypothesis), axis=1))
# Try to change learning_rate to small numbers
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)
# Correct prediction Test model
prediction = tf.argmax(hypothesis, 1)
is_correct = tf.equal(prediction, tf.argmax(Y, 1))
accuracy = tf.reduce_mean(tf.cast(is_correct, tf.float32))
# Launch graph
with tf.Session() as sess:
# Initialize TensorFlow variables
sess.run(tf.global_variables_initializer())
for step in range(201):
cost_val, W_val, _ = sess.run([cost, W, optimizer], feed_dict={X: x_data, Y: y_data})
print(step, cost_val, W_val)
# predict
print("Prediction:", sess.run(prediction, feed_dict={X: x_test}))
# Calculate the accuracy
print("Accuracy: ", sess.run(accuracy, feed_dict={X: x_test, Y: y_test}))일단 실습 전체 코드
학습이 잘 되었을 때에도 NaN이란걸 마주칠 수 있다.
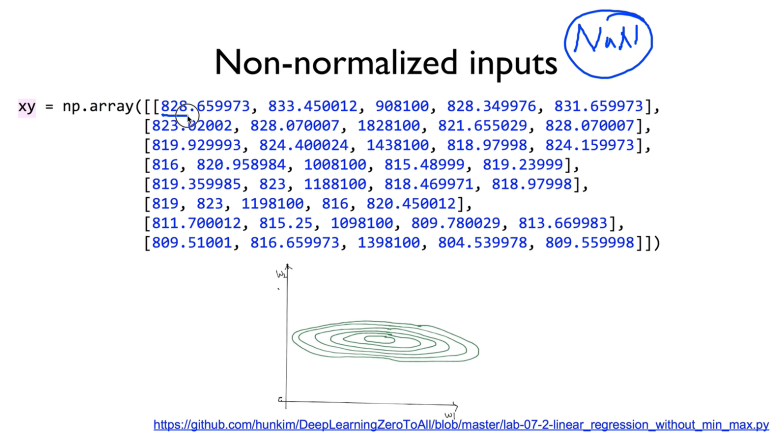
저렇게 큰 값들이 주어지면 cost function이 저렇게 치우치게 그려질 수 있다.
왜곡이 심하면 바깥으로 튕겨져 나갈 수도 있다.

실제로 코드는 잘만 짜여져 있는데 출력이 이상할 수 있다.
왜냐하면 데이터 값들의 차가 너무 큰데
normalized 를 안했기 때문이다.
import tensorflow.compat.v1 as tf
import numpy as np
tf.disable_v2_behavior()
xy = np.array([[828.659973, 833.450012, 908100, 828.349976, 831.659973],
[823.02002, 828.070007, 1828100, 821.655029, 828.070007],
[819.929993, 824.400024, 1438100, 818.97998, 824.159973],
[816, 820.958984, 1008100, 815.48999, 819.23999],
[819.359985, 823, 1188100, 818.469971, 818.97998],
[819, 823, 1198100, 816, 820.450012],
[811.700012, 815.25, 1098100, 809.780029, 813.669983],
[809.51001, 816.659973, 1398100, 804.539978, 809.559998]])
x_data = xy[:, 0:-1]
y_data = xy[:, [-1]]
# placeholders for a tensor that will be always fed.
X = tf.placeholder(tf.float32, shape=[None, 4])
Y = tf.placeholder(tf.float32, shape=[None, 1])
W = tf.Variable(tf.random_normal([4, 1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')
# Hypothesis
hypothesis = tf.matmul(X, W) + b
# Simplified cost/loss function
cost = tf.reduce_mean(tf.square(hypothesis - Y))
# Minimize
optimizer = tf.train.GradientDescentOptimizer(learning_rate=1e-5)
train = optimizer.minimize(cost)
# Launch the graph in a session.
sess = tf.Session()
# Initializes global variables in the graph.
sess.run(tf.global_variables_initializer())
for step in range(101):
cost_val, hy_val, _ = sess.run(
[cost, hypothesis, train], feed_dict={X: x_data, Y: y_data})
print(step, "Cost: ", cost_val, "\nPrediction:\n", hy_val)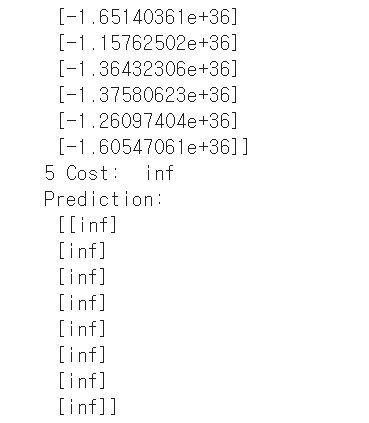
이것을 해결하는 방법은 normalize를 하거나 MinMaxScaler() 라는 함수를 쓰는거다.

MinMaxScaler()는 원래 데이터의 값들을 0과 1사이의 값들로 다 바꿔주는 역할을 한다.
아까와 다르게 cost funciton 그래프가 동그래졌다(왜곡이 적어짐)
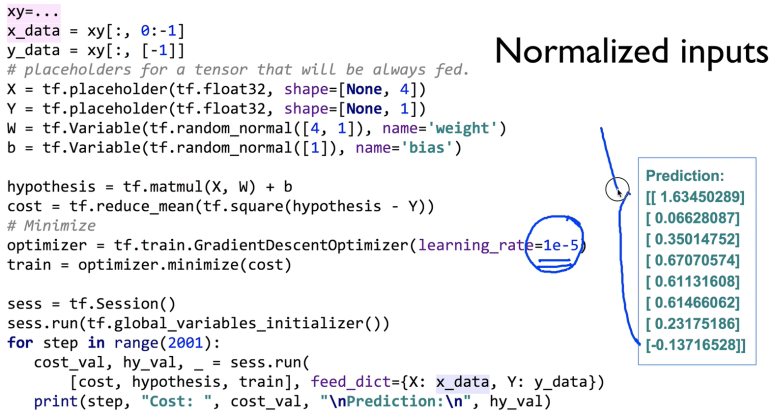
똑같은 소스코드지만 normalize를 해주었더니 아까와 다르게 결과가 잘 되는 것을 볼 수 있다.
import tensorflow.compat.v1 as tf
import numpy as np
tf.disable_v2_behavior()
def min_max_scaler(data):
numerator = data - np.min(data, 0)
denominator = np.max(data, 0) - np.min(data, 0)
# noise term prevents the zero division
return numerator / (denominator + 1e-7)
xy = np.array(
[
[828.659973, 833.450012, 908100, 828.349976, 831.659973],
[823.02002, 828.070007, 1828100, 821.655029, 828.070007],
[819.929993, 824.400024, 1438100, 818.97998, 824.159973],
[816, 820.958984, 1008100, 815.48999, 819.23999],
[819.359985, 823, 1188100, 818.469971, 818.97998],
[819, 823, 1198100, 816, 820.450012],
[811.700012, 815.25, 1098100, 809.780029, 813.669983],
[809.51001, 816.659973, 1398100, 804.539978, 809.559998],
]
)
# very important. It does not work without it.
xy = min_max_scaler(xy)
print(xy)x_data = xy[:, 0:-1]
y_data = xy[:, [-1]]
# placeholders for a tensor that will be always fed.
X = tf.placeholder(tf.float32, shape=[None, 4])
Y = tf.placeholder(tf.float32, shape=[None, 1])
W = tf.Variable(tf.random_normal([4, 1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')
# Hypothesis
hypothesis = tf.matmul(X, W) + b
# Simplified cost/loss function
cost = tf.reduce_mean(tf.square(hypothesis - Y))
# Minimize
train = tf.train.GradientDescentOptimizer(learning_rate=1e-5).minimize(cost)
# Launch the graph in a session.
with tf.Session() as sess:
# Initializes global variables in the graph.
sess.run(tf.global_variables_initializer())
for step in range(101):
_, cost_val, hy_val = sess.run(
[train, cost, hypothesis], feed_dict={X: x_data, Y: y_data}
)
print(step, "Cost: ", cost_val, "\nPrediction:\n", hy_val)이건 실습한 코드
